Stochastic Process

based on the lecture: Syllabus | Topics in Mathematics with Applications in Finance | Mathematics | MIT OpenCourseWare

A Stochastic Process is a collection of random variables indexed by time.

We have two types of these processes, discrete-time processes and continuous-time processes.

$$\{\begin{array}{ll}\text{Discrete-Time Stochastic Process}& \text{if the index set is countable (e.g., }t=0,1,2,\dots \text{)}\\ \text{Continuous-Time Stochastic Process}& \text{if the index set is uncountable (e.g., }t\in [0,\infty )\text{)}\end{array}$$

Note that the function which represents a continuous-time stochastic process itself does not need to be a continuous time, rather it just means there is an uncountable number of random variables indexed by time.

Alternate Definition

A Stochastic Process is a probability distribution over a space of paths.

Examples

Example 1

$$f(t)=t\text{with probability 1}$$

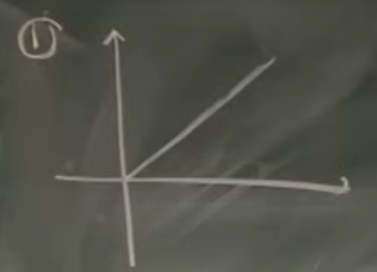
This is a straight forward example, where it’s just a single deterministic path.

Example 2

$$\{\begin{array}{ll}f(t)=t& \text{with probability }0.5\\ f(t)=-t& \text{with probability }0.5\end{array}$$

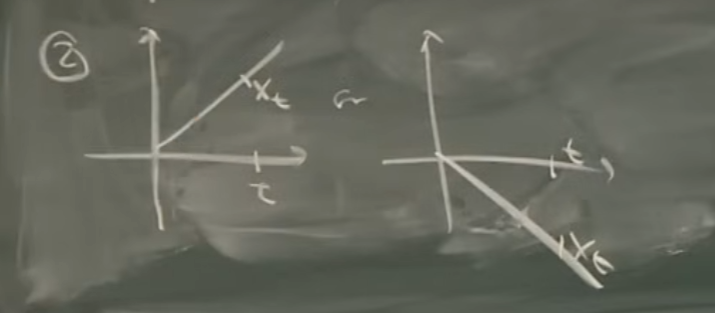
This example has two possible paths, one where the function increases linearly and another where it decreases linearly, each with equal probability. Like a coin flip, we can think of this stochastic process as randomly selecting one of these two paths at the start and following it through time.

Example 3

$$\text{for each }t,f(t)=\{\begin{array}{ll}t& \text{with probability }0.5\\ -t& \text{with probability }0.5\end{array}$$

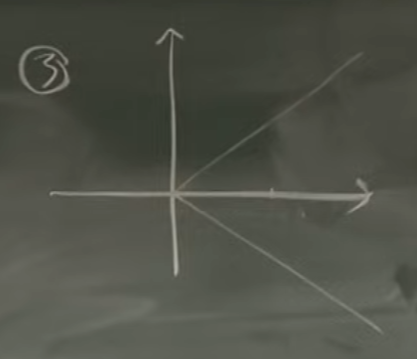
This last one, you can imagine two translucent lines, one at $f(t)=t$ the other at $f(t)=-t$, and at each time step, the stochastic process randomly selects one of these two lines to be on. Over time, this results in a zig-zagging path that jumps between the two lines at each time step an infinite number of times.