Orthogonal Projection

In linear algebra, an orthogonal projection is a linear transformation which maps a vector to a vector space such that the difference between the original vector and the projected vector is orthogonal to the vector space.

More formally, we can define a projection of $\vec{y}$ onto a subspace of ${\mathbb{R}}^n$ $W$ written as

$${\mathrm{proj}}_W(\vec{y})=\hat{y}$$

where $\hat{y}\in W$ and $\vec{y}-\hat{y}$ is orthogonal to every vector in $W$. This is written as

$$\vec{y}-\hat{y}\perp W$$

In human terms, $\hat{y}$ is the vector in $W$ that is closest to $\vec{y}$.

Geometric Interpretation

Geometrically, the orthogonal projection of a vector $\vec{y}$ onto a subspace $W$ can be visualized as dropping a perpendicular from the tip of $\vec{y}$ to the subspace $W$. The point where this perpendicular intersects $W$ is the projected vector $\hat{y}$.

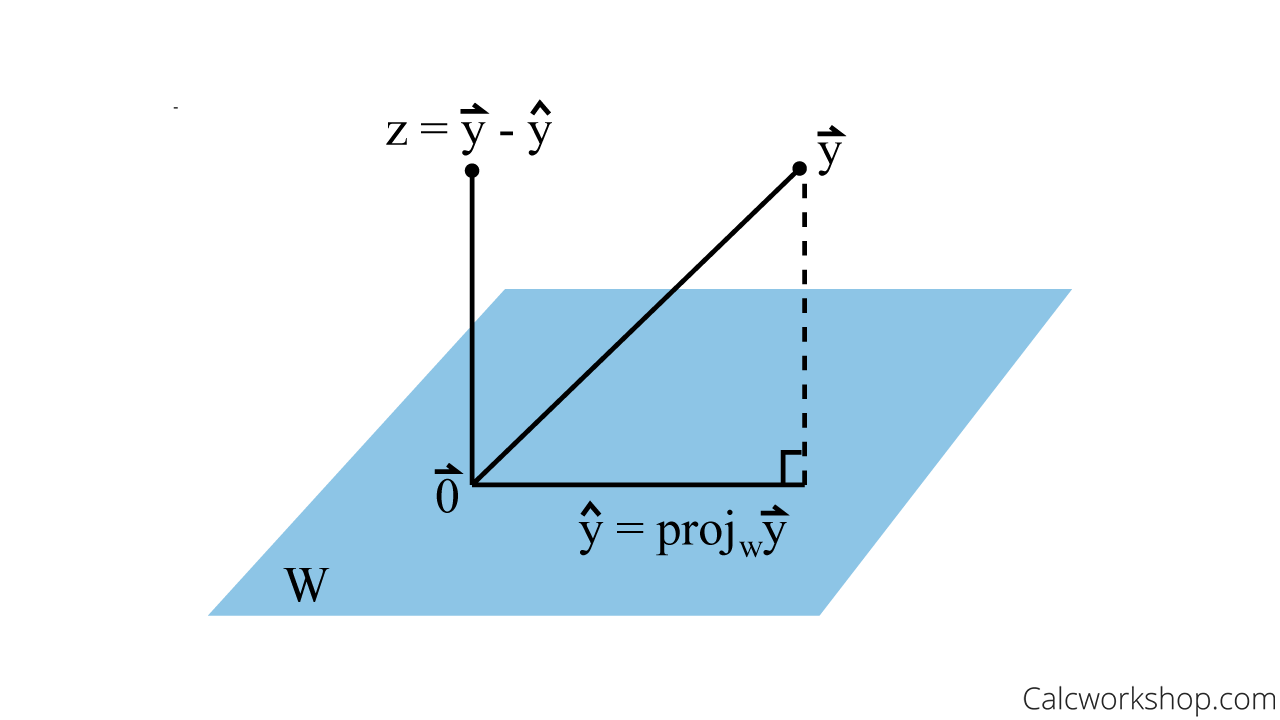
Examples

Example 1

Consider two vectors

$$\overrightarrow{u_1}=\left[\begin{array}{c}2\\ 5\\ -1\end{array}\right],\overrightarrow{u_2}=\left[\begin{array}{c}-2\\ 1\\ 1\end{array}\right]$$

Then we can say that $\overrightarrow{u_1}$ and $\overrightarrow{u_2}$ are orthogonal vectors as $\overrightarrow{u_1}\cdot \overrightarrow{u_2}=0$. We then define a subspace $W$ and an orthogonal basis $B$ for $W$ as:

$$W=\mathrm{span}\{\overrightarrow{u_1},\overrightarrow{u_2}\},B=\{\overrightarrow{u_1},\overrightarrow{u_2}\}$$

Now our task is to find ${\mathrm{proj}}_W\vec{y}$ given

$$\vec{y}=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

We start by calculating ${\mathrm{proj}}_W\vec{y}$ using the formula for projection onto an orthogonal basis:

$${\mathrm{proj}}_W\vec{y}=\frac{\vec{y}\cdot \overrightarrow{u_1}}{\overrightarrow{u_1}\cdot \overrightarrow{u_1}}\overrightarrow{u_1}+\frac{\vec{y}\cdot \overrightarrow{u_2}}{\overrightarrow{u_2}\cdot \overrightarrow{u_2}}\overrightarrow{u_2}$$

Calculating the dot products:

$${\mathrm{proj}}_W\vec{y}=\frac{2+10-3}{4+25+1}\cdot \left[\begin{array}{c}2\\ 5\\ -1\end{array}\right]+\frac{-2+2+3}{4+1+1}\cdot \left[\begin{array}{c}-2\\ 1\\ 1\end{array}\right]$$ $${\mathrm{proj}}_W\vec{y}=\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]$$

Therefore

$$\vec{z}=\vec{y}-{\mathrm{proj}}_W\vec{y}=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]-\left[\begin{array}{c}\frac{-2}{5}\\ 2\\ \frac{1}{5}\end{array}\right]=\left[\begin{array}{c}\frac{7}{5}\\ 0\\ \frac{14}{5}\end{array}\right]$$

$\vec{z}$ should then be an orthogonal vector to both ${\mathrm{proj}}_W\vec{y}$ and every element of $B$.