Theorem - All NFAs have an equivalent DFA

Statement

Every Nondeterministic Finite Automaton has an equivalent Deterministic Finite Automaton.

Proof

To show every NFA has an equivalent DFA, it would be sufficient to prove the existence of a general algorithm to covert any NFA to an equivalent DFA.

We begin by reviewing each component of the definition of a DFA to see what needs to be “adjusted.”

Step 1: States

The first thing to consider is the finite set of states $Q$. In an NFA, the computation can be in a combination of states at the same time. In a DFA it can only be in one state at any time. IDEA: let sets of states in an NFA each be a single state in the corresponding DFA.

Example: suppose an NFA transitions to states $q_0$ and $q_1$. In our corresponding DFA we can define an “amalgamated” or “unified” state. How many such states do we need? If our NFA has $|Q_N|=k$ states, our DFA has $|Q_D|=\mathcal{P}(Q_N)=2^{|Q_N|}$.

This is the complete set of states that our DFA could possibly use. Of course as we fill in the transition table we may find some (or even most) states go unused.

Step 2: Alphabet

The alphabet stays the same: ${\sum }_N={\sum }_D$

Step 3: Starting State

Let $q_0\in Q_N$ be the starting state of our NFA. The starting state of the corresponding DFA is $\{q_0\}\cup \delta (q_0,\epsilon )$, i.e., combination of $q_0$ and any other states reachable from $q_0$ by an $\epsilon$-transition.

Step 4: Final States

Let $F_N$ be the set of final states of our NFA. Recall the NFA accepts if any of the computational paths accepts. Taking this over to the DFA means designating any of the “amalgamated” states as accept if they contain some $q_i\in F_N$. Example: if $F_N=\{q_1\}$ then $F_D=\{\{q_1\},\{q_1,q_0\},\{q_1,q_2\},\{q_0,q_1,q_2\}\}$

Human: essentially, if any “amalgamated” state contains any previously accepted state, then this new state is also accepted.

Step 5: Transition Function

Filling in the transition function ${\delta }_D$ proceeds in two parts.

Part 1 we write a table with single states for rows and letters for columns. We use the NFA’s transition function ${\delta }_N$ to fill in this table converting sets of states to “amalgamated” states. But we still have to account for $\epsilon$-transitions (Epsilon Transitions). The way we do this is as follows: if we transition from a state $q_i$ to a state $q_j$, and $q_j$ contains an $\epsilon$-transitions to state $q_k$, then in effect $q_i$ transitions to $\{q_j\}\cup \{q_k\}$. This continues recursively until there are no new $\epsilon$-transitions to follow.

Step 2 Now that we have the transitions for the single states written, we add new rows to the table corresponding to the amalgamated states i.e., ($\{\{q_0,q_1\},\{q_0,q_2\}\}$, etc.). We fill in these cells by taking the union of the cells of the corresponding single states. E.g. to fill in the cell ${\delta }_D(\{q_0,q_1\},a)$ we take ${\delta }_D(\{q_0,a\})\cup \delta D(\{q_1\},a)$.

Example

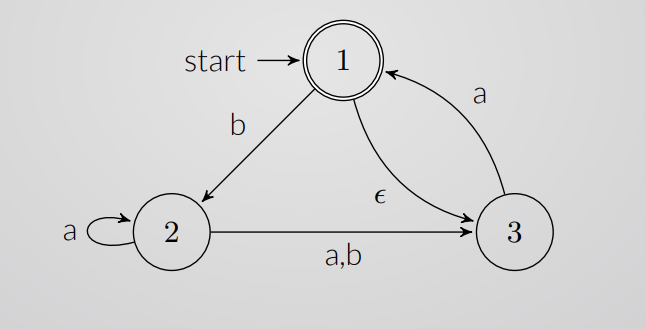
States and Alphabet

1. States.
   $Q_D$ will end up being some subset of the powerset of $Q_N$, i.e.,

   $$Q_D\subset \mathcal{P}(Q_N)$$

2. Alphabet.

   $${\Sigma }_D={\Sigma }_N=\{a,b\}$$

3. Start state.
   The NFA’s start state is $1$, but there’s an $ϵ$-transition to $3$.
   The DFA’s start state, therefore, is the amalgamated state $\{1,3\}$.

4. Final states.

   $$F_N=\{1\},F_D=\{\{1\},\{1,2\},\{1,3\},\{1,2,3\}\}$$

---

Transition function (single states)

In part 1 of the conversion we start out by writing out the transitions for the single states, taking into account the $ϵ$-transitions:

$$\begin{array}{ccc}& a& b\\ \{1\}& \varnothing & \{2\}\\ \{2\}& \{2,3\}& \{3\}\\ \{3\}& \{1,3\}& \varnothing \end{array}$$

---

Transition function (amalgamated states)

Now we fill in the rest of the amalgamated states by taking the unions of the single states:

$$\begin{array}{ccc}& a& b\\ \{1\}& \varnothing & \{2\}\\ \{2\}& \{2,3\}& \{3\}\\ \{3\}& \{1,3\}& \varnothing \\ \{1,2\}& \{2,3\}& \{2,3\}\\ \{1,3\}& \{1,3\}& \{2\}\\ \{2,3\}& \{1,2,3\}& \{3\}\\ \{1,2,3\}& \{1,2,3\}& \{2,3\}\end{array}$$

---

Minimization

We’re using more states than we need. We can eliminate any state where there is no combination that leads us to them, and is not a starting state.

In the example above, the states $\{1\}$ and $\{1,2\}$ fit this definition. So we can eliminate them.

---

Result