Nondeterministic Finite Automata

Nondeterministic Finite Automata (NFA)

A type of Finite Automaton which is nondeterministic. This means that the transition Function $Q$ may contain zero, one, or more output for each possible character in the Alphabet.

Definition

Formally, an FA is a 5-tuple $(Q,\Sigma ,\delta ,q_0,F)$:

1. $Q$: a finite Set of states
2. $\Sigma$: a finite Alphabet
3. $\delta :Q\times (\Sigma \cup \{ϵ\})\to \mathcal{P}(Q)$: a transition Relation
4. $q_0\in Q$: the start state
5. $F\subseteq Q$: a set of accepting states

Human Definition An NFA is like a DFA, but:

• From one state and input, the machine may have multiple possible next states.
• It may even move without consuming input (ε-transitions).
• A String is accepted if at least one path leads to an accepting state once the entire string is consumed.

Example 1

An NFA that accepts strings of $\{0,1\}$ that end in $01$:

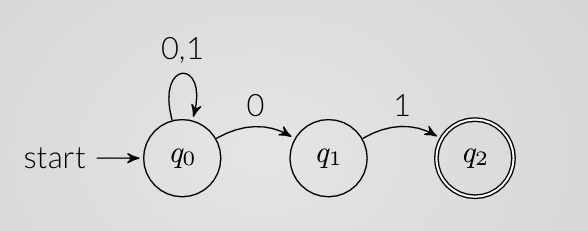
Formally defined as: $A=(\{q_0,q_1,q_2\},\{0,1\},\delta ,q_0,\{q_2\})$ where $\delta =$

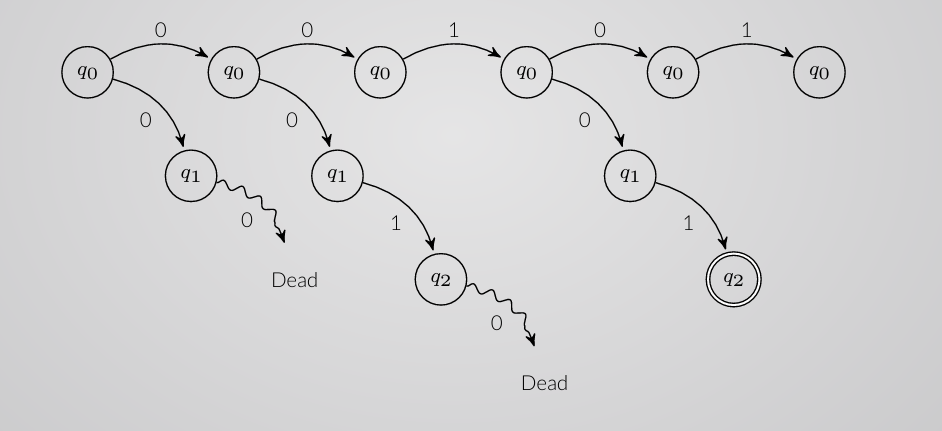
& 0 & 1 \\ \hline q_0 & \set{q_0,q_1} & \set{q_0} \\ q_1 & \varnothing & \set{q_2} \\ q_{2} & \varnothing & \varnothing \\ \end{array}$$ Example of processing: ![[99 Attachments/Pasted image 20250917170730.png]] As at least one path accepting the string, this string is accepted by the NFA. ## Example 2 Example containing [[10 Zettels/20250917-171108|Epsilon Transitions]] ![[99 Attachments/Pasted image 20250917171246.png]] The above state machine matches any set of strings (build of capital letters) ending in "ING" or "ER".