Regular Language Closure

Definition

Let $\mathcal{R}\mathcal{EG}$ be the set of regular language. Let $f(\dot{)}$ be an operation that accepts one (or more) languages and produces a language. We say the set of regular languages $\mathcal{R}\mathcal{EG}$ is closed under $f(\dot{)}$ if, for all $L_1,\dots ,L_n\in \mathcal{R}\mathcal{EG}$, it is the case that $f(L_1,\dots ,L_n)\in \mathcal{R}\mathcal{EG}$.

Examples

Regular languages are closed under a variety of operations:

• Compliment: $L^{\prime }=\{s:s\notin L\}$
• Reversal: $L^{\prime }=\{s:\mathrm{reverse}(s)\in L\}$
• Union: $L^{\prime }=\{s:s\in L_1\text{ or }s\in L_2\}$
• Intersection: $L^{\prime }=\{s:s\in L_1\text{ and }s\in L_2\}$
• and many more…

Proofs of Closures

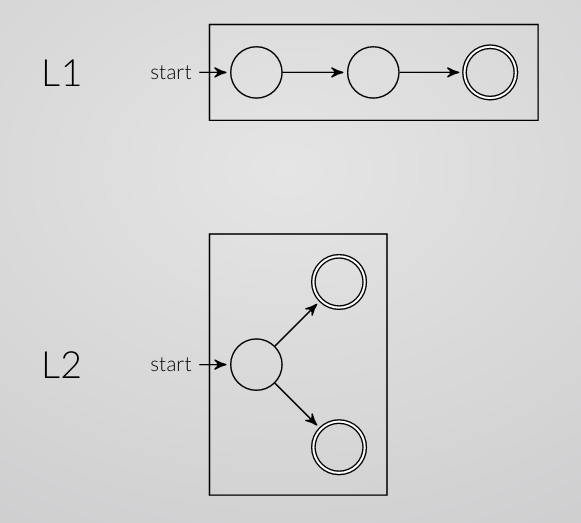
Lets start all proofs with the following NFAs.

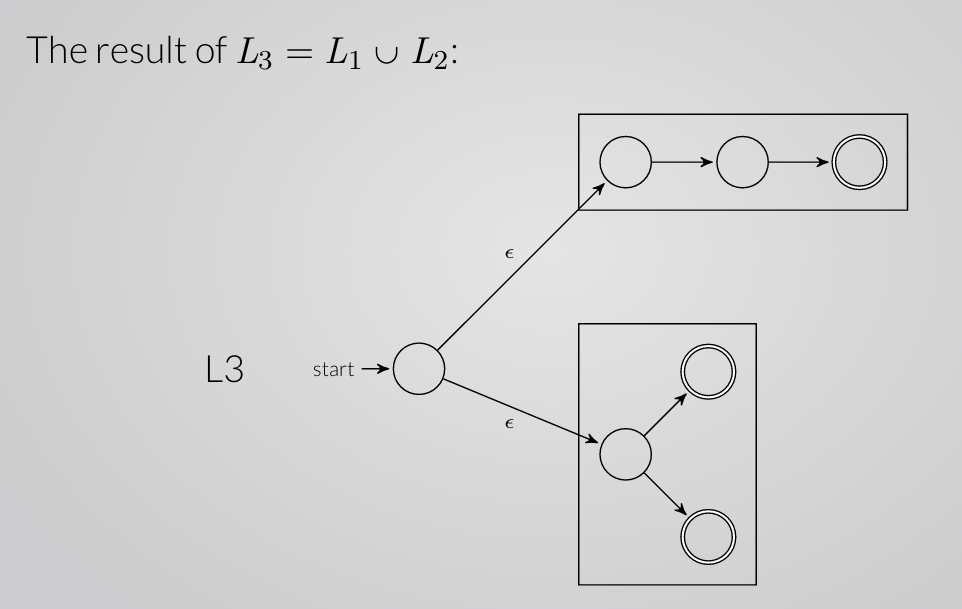
Union of Languages

Let $L_3=L_1\cup L_2$, we can construct the new NFA by:

1. Define a new “joint” start state
2. Add Epsilon Transitions from the new join start state into the start states of $L_1$ and $L_2$.
3. Convert the start states of $L_1$ and $L_2$ to non-starting states.